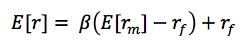"Alpha's Measurement Problem"

From Newfound Research:

Alpha's measurement problem 

Summary

• Alpha is the holy grail of asset management: risk-free excess returns generated by investment skill.
   
• Alpha is one of the most commonly quoted summary statistics – yet measuring alpha is surprisingly difficult.
   
• Without an understanding of measurement uncertainty, fit of our model, or even the risk factors utilized to calculate alpha, the statistic loses its applicability.

Sweat, tears – and likely even blood – have been spilled over what is really just the intercept value in a linear regression.

We’re talking about alpha, of course.

 

For a mathematician, alpha is nothing special.  We can only presume that one day, someone from a marketing department walked by a bunch of quants huddled around a white board and asked a question that would forever change history: “what’s that Greek letter?”

At the intersection of mathematics and finance, alpha is defined as the excess return generated by an investment process beyond what would be predicted by an equilibrium model like the capital asset pricing model (“CAPM”). 

The CAPM tells us that the equilibrium (or expected) return of a security is proportional to its systematic, or non-diversifiable, risk. 

Theory Side Note: You might be asking why the CAPM - and many similar models - assume that investors are compensated for systematic risk, but not idiosyncratic risk.  Idiosyncratic risk is by definition diversifiable.  If idiosyncratic risk was compensated, then investors could earn positive returns with zero risk. How?  They could simultaneously hold a large number of securities, diversifying away any idiosyncratic risk, and hedge away any exposure to systematic risk.  This creates an arbitrage that would quickly be exploited and eliminated. Therefore, investors cannot be compensated for idiosyncratic risk.

In equation form, CAPM gives us the following:

 

Translating into English: the expected return of the strategy or security is equal to the risk-free rate plus a premium that is proportional to broad market exposure.  The proportionality constant is the other familiar Greek letter – beta.  Again, we expect to earn return based on exposure to broad market risk and nothing else.

Now, what returns the portfolio actually realizes over any given period may be very different than what the equilibrium model would predict.  We can compute the difference as:  

 

If that difference is consistently above zero, we’ve discovered positive alpha! 

Positive alpha is attractive because, in theory, we could hedge our exposure to systematic risks and be left only with pure, risk-free returns.  While most investors do not actually do this, they do use alpha as a measure of a manager’s ability.  If the manager has skill in selection or allocation, we would expect that skill to emerge as positive excess risk-adjusted returns.  In other words, alpha. 

The problem is that while this may be theoretically true, the mechanics of trying to measure alpha leave much to be desired.  At worst, relying on traditional reports of alpha may be downright misleading for investors making allocation decisions.

Alpha has Uncertainty

To estimate alpha, investors typically run a linear regression of excess strategy returns against excess market returns.  The setup usually looks something like this:

To interpret the equation: monthly excess strategy returns are modeled as being equal to a constant value (alpha) plus exposure to systematic return (beta) plus some noise (epsilon). 

With enough monthly return data, the values for alpha and beta can be estimated in a manner where noise is minimized, in effect allowing alpha and beta to explain as much of the monthly excess returns as possible....MUCH MORE