A Design Dilemma Solved, Minus Designs

A 150-year-old conundrum about how to group people has been solved, but many puzzles remain.
In 1850, the Reverend Thomas Kirkman, rector of the parish of Croft-with-Southworth in Lancashire, England, posed an innocent-looking puzzle in the Lady’s and Gentleman’s Diary, a recreational mathematics journal:
“Fifteen young ladies in a school walk out three abreast for seven days in succession: it is required to arrange them daily, so that no two shall walk twice abreast.” (By “abreast,” Kirkman meant “in a group,” so the girls are walking out in groups of three, and each pair of girls should be in the same group just once.)
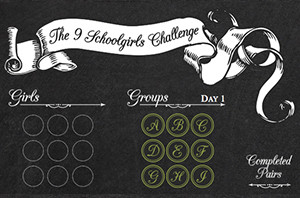
The Nine Schoolgirls Challenge:
Solve a variation of Thomas Kirkman’s puzzle by arranging nine girls in walking groups. And think fast — the clock is ticking.
Pull out a pencil and paper, and you’ll quickly find that the problem is harder than it looks: After arranging the schoolgirls for the first two or three days, you’ll almost inevitably have painted yourself into a corner, and have to undo your work.
The puzzle tantalized readers with its simplicity, and in the years following its publication it went viral, in a slow, modestly Victorian sort of way. It generated solutions from amateurs (here’s one of seven solutions) and papers by distinguished mathematicians, and was even turned into a verse by “a lady,” that begins:
A governess of great renown,
Young ladies had fifteen,
Who promenaded near the town,
Along the meadows green.
While Kirkman later bemoaned the fact that his weightier mathematical contributions had been eclipsed by the popularity of this humble brainteaser, he was quick to defend his territory when another prominent mathematician, James Joseph Sylvester, claimed to have created the problem “which has since become so well-known, and fluttered so many a gentle bosom.”
The puzzle may seem like an amusing game (try a simpler version here), but its publication helped launch a field of mathematics called combinatorial design theory that now fills gigantic handbooks. What started as an assortment of conundrums about how to arrange people into groups — or “designs,” as these arrangements came to be called — has since found applications in experiment design, error-correcting codes, cryptography, tournament brackets and even the lottery."Design theory may even have been used by betting cartels that made millions of dollars off of Massachusetts’ poorly designed Cash WinFall lottery between 2005 and 2011. That lottery involved choosing six numbers out of 46 choices; tickets won a jackpot if they matched all six numbers, and smaller prizes if they matched five out of six numbers."
Yet for more than 150 years after Kirkman circulated his schoolgirl problem, the most fundamental question in the field remained unanswered: Do such puzzles usually have solutions? Kirkman’s puzzle is a prototype for a more general problem: If you have n schoolgirls, can you create groups of size k such that each smaller set of size t appears in just one of the larger groups? Such an arrangement is called an (n, k, t) design. (Kirkman’s setup has the additional wrinkle that the groups must be sortable into “days.”)The Nine Schoolgirls Challenge
It’s easy to see that not all choices of n, k and t will work. If you have six schoolgirls, for instance, you can’t make a collection of schoolgirl triples in which every possible pair appears exactly once: Each triple that included “Annabel” would contain two pairs involving her, but Annabel belongs to five pairs, and five is not divisible by two. Many combinations of n, k and t are instantly ruled out by these sorts of divisibility obstacles.
For the parameters that aren’t ruled out, there’s no royal road to finding designs. In many cases, mathematicians have found designs, through a combination of brute force and algebraic methods. But design theorists have also found examples of parameters, such as (43, 7, 2), that have no designs even though all the divisibility requirements check out. Are such cases the exception, mathematicians wondered, or the rule? “It was one of the most famous problems in combinatorics,” said Gil Kalai, a mathematician at the Hebrew University of Jerusalem. He recalls debating the question with a colleague a year and a half ago, and concluding that “we’ll never know the answer, because it’s clearly too hard.”...MORE