This will be the last Uncertainty Wednesday for 2017 as I am about to go away on vacation. In the last post I had introduced the idea that sometimes when volatility is suppressed it comes back to bite us. I wanted to have a really simple model for demonstrating that and so I wrote some Python code to make a 50:50 coin toss and depending on the result either increment or decrement a value by +/- 2 (I set the initial value to 100). Here is a plot of a sample run:
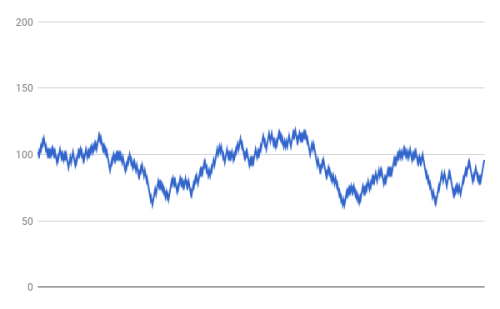
Now to suppress volatility, I modified the program so that it would increment or decrement the value by +/- 1 instead, i.e. half the original change. I then added the suppressed +/- 1 (the other half of the change) into a “buffer” – accumulating +1 in a positive buffer and -1 in a negative buffer. I then gave each buffer a 1 in 1,000 chance of being released. Here is a plot where the buffer is not released:
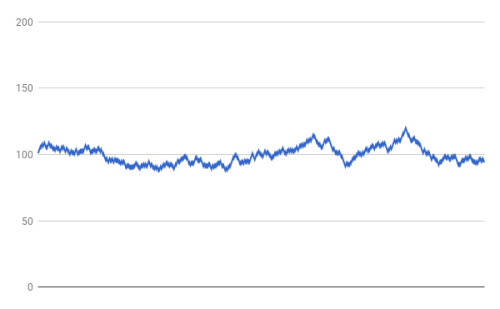
We can immediately see that there is less volatility. In fact, when we determine the sample variance, the sample in the first chart comes in at 178 whereas the sample in the second chart has a variance of only 42.
Here by contrast is a plot from a run where the negative buffer gets released.
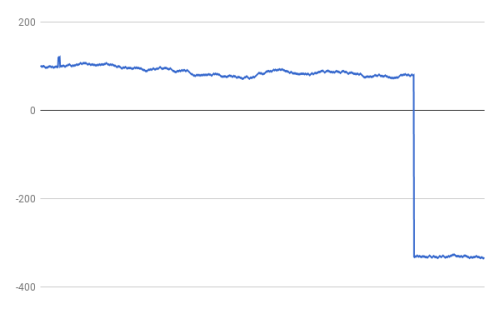
We can see that once again the chart starts out looking as if it has rather low volatility. But then all of a sudden all the suppressed down movements are being realized in one go and the value drops dramatically....MOREOh dear.
Speaking of seeing past misdirection (post immediately below), Mr. Wenger's January 17th 2018 Uncertainty Wednesday' post contains a simple sentence with profound implications:
"...For any fat tailed distribution, the sample variance will underestimate the true variance. Mistaking the sample variance for the actual variance is the same error as mistaking the sample mean for the actual mean...."Here's Contiuations' homepage.