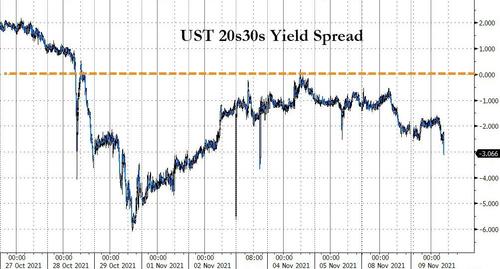
ZeroHedge first noted this oddity on October 28, GDP report day; and then again this morning:
....And the long-end of the curve remains inverted for the 9th straight day...
The dollar is down as yields drop...
And here with some higher level discussion than I can muster is Bond Economics (also on blogroll at right):
I have seen a certain amount of chatter about inversions of the long end (or ultra-long end) of the Treasury curve. I do not have enough information to offer definitive conclusions on recent market action, but in the article I explain why I view a 20-/30-year inversion is not comparable to a 2-/10-year inversion.
Terminology Clarification
The first thing to note that I use the terms “term premium” and “technical factors” in a fashion that is consistent with market practitioners, and not academics in finance and economics.
Using my terminology, we can decompose an observed bond yield as:
Bond yield = expected path of overnight funding cost + term premium + technical factors.
Academics decompose into two terms.
Bond yield = expected path of overnight funding cost + term premium.
The problem with the academics’ version is that it lumps in all deviations from the expected path into the “term premium” — including other factors that are quantifiable.
For example, imagine that some tax change caused bond yields at the 20+ maturity range to rise by 20 basis points. Under the academics’ definition, the “term premium” rose by 20 basis points. From my perspective, that was a new technical factor, and is independent of the premium demanded for taking duration risk — which is the usual interpretation of “term premium.” Academics might argue that such directly quantifiable factors should be first removed from pricing before extracting curves, but what about factors that have a “fuzzier” effect on yields?
Since this article discussed “technical factors” that affect observed yields, this difference in point of view needs to be kept in mind.
Another terminology point: when I write “duration,” I mean the modified duration (or adjusted duration), and not the Macaulay duration (which is the weighted average maturity of a bond’s cash flows).
Why Would the 30-Year Yield Be Lower than 20-Year Yield?
If we ignored technical factors, it seems unusual that the 30-year yield would be lower than the 20-year: why would the market discount rate cuts starting 20-years in the future? Even though I am rate expectations zealot, I do not think that is the correct interpretation. Instead, we need to look at what I term “technical factors.”
I will divide this analysis into five main areas: term premium, issuance strategy, liquidity, “duration demand,” and convexity. The convexity factor is one that is the least obvious to people who are unfamiliar with bond markets, but I will deal with the more familiar ones first.
Term Premium?
If we use my definition of the term premium as being solely the extra premium demanded to take duration risk, it is not entirely clear what the shape of the ultra-long premium should be. Once you are out at the 20 year maturity, why is going to 30 years more risky? This is quite different than looking at overnight duration versus six months, etc.
If we wanted to come up with a different price of risk for the 20-year versus the 30-year, we run into the factors that come up in later sections of the article.....
....MUCH MORE
Mr. Romanchuk knows this stuff.