As nature scales, complexity gives way to universal law.
Here’s how to cause a ruckus: Ask a bunch of naturalists to simplify the world. We usually think in terms of a web of complicated interactions among animals, plants, microbes, earth, wind, and fire—what Darwin called “the entangled bank.” Reducing the bank’s complexity to broad generalizations can seem dishonest.
So when Tony Ives, a theoretical ecologist at the University of Wisconsin, prodded his colleagues at the 2013 meeting of the Ecological Society of America by calling for a vote on whether they ought to seek out general laws, it probably wasn’t surprising that two-thirds of the room voted no.1
Despite the skepticism, the kinds of general laws made possible by simplification have remarkable predictive powers. They could let us calculate how many species there are in ecosystems that are too big to sample thoroughly, or how many will be lost after habitat destruction.
Perhaps because I started in biology after training in physics, I’m an ecologist who finds beauty in these general laws. In physics, the last thing you’d worry about are differences between one molecule of a gas and another. No one has a personal favorite electron. The ideal gas law relating pressure, volume, and temperature holds equally well for oxygen and nitrogen. Phase transitions between liquids and gases behave in the same way as the magnetization of certain metals.
Why shouldn’t an ecosystem be just as beautifully perfect as an ideal gas, and why can’t ecologists have as much predicting power as a physicist? The answers to these questions just might be “it is,” and “they can.” But only when viewed from a particular perspective.
In the 1980s, two ecologists, Jim Brown at the University of New Mexico and Brian Maurer at Brigham Young University, coined the term macroecology, which gave a name and intellectual home to researchers searching for emergent patterns in nature. Frustrated by the small scale of many ecological studies, macroecologists were looking for patterns and theories that could allow them to describe nature broadly in time and space.
Brown and Maurer had been influenced heavily by regularities in many ecological phenomena. One of these, called the species-area curve, was discovered back in the 19th century, and formalized in 1921. That curve emerged when naturalists counted the number of species (of plants, insects, mammals, and so on) found in plots laid out in backyards, savannahs, and forests. They discovered that the number of species increased with the area of the plot, as expected. But as the plot size kept increasing, the rate of increase in the number of species began to plateau. Even more remarkable, the same basic species-area curve was found regardless of the species or habitat. To put it mathematically, the curve followed a power law, in which the change in species number increased proportionally to the square root of the square root of the area.
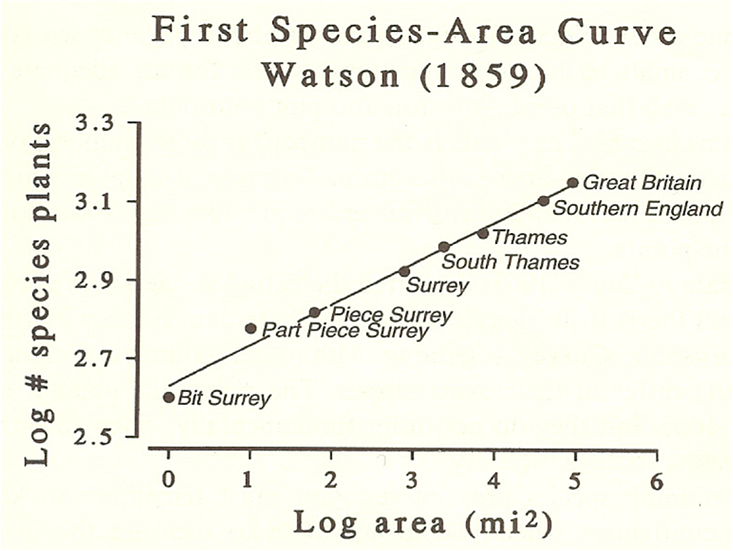
Power laws are common in science, and are the defining feature of universality in physics. They describe the strength of magnets as temperature increases, earthquake frequency versus size, and city productivity as a function of population. For many ecologists, the species-area curve strikes a nerve. It suggests that at a large enough scale, the specific detail of an ecosystem—the “entangled bank” that lies so near and dear to the ecologist’s heart—simply doesn’t matter. The idiosyncrasies wash out, and ecological systems start to look surprisingly similar to a broad swathe of disparate systems in other sciences.If interested:
The universality of the species-area curve became abundantly clear in the models ecologists built to understand it. In 2001, an ecologist then at Princeton University, Steve Hubbell, developed a model based on the radical assumption that any selective differences (differences which give an evolutionary advantage or disadvantage) between individuals in the same part of a food chain are irrelevant. That means that individual outcomes are a kind of ecological roulette. Some species get lucky, ending up with broad, abundant distributions across space, while other species become relatively rare. Through a combination of analytical equations and computer simulations, his model, called the unified neutral theory of biodiversity, predicted a species-area curve that looked surprisingly realistic. Its success was built on this brutally simplified version of real ecosystems, with plants, animals, and organisms replaced by nearly identical statistical placeholders.
Another ecologist with physics training, John Harte, wondered if the species-area curve could be understood with even less ecological mechanism than the neutral theory supposed. Harte developed the maximum entropy theory of ecology, based around ideas taken from thermodynamics and information theory. Entropy is a measure of the disorder of a system, and is used in thermodynamics to calculate the most likely arrangement of identical gas molecules in a fixed volume. More disorder usually wins. By playing with the spatial distribution of species under certain constraints, Harte used maximum entropy theory to predict the number of tree species across the entire Western Ghats mountain range in India. Their estimate, published in Ecology Letters, fell within a respectable 10 percent of some 900 types of counted trees.2 Harte wasn’t considering the details of individual trees and their reproduction or seed dispersal—his work was purely driven by principles from the realm of information theory....MORE
Financial Physics: "Power laws in finance"
Scientific American: "Can Math Beat Financial Markets?"
"The Philosophy of Complexity: Are Complex Systems Inherently Tyrannical?"
Yes.Economists and Econophysics
In the end the universe itself is inherently tyrannical.
You are not the boss....