Complexity: Travel Routes and the Organization of Cities

First posted in February 2018:
In January's "A conversation about how public transport really works" I mentioned:

My interest in transport planning is usually the financial angle,* maybe quasi-esoteric complexity stuff e.g. "Study on Fractal Features of Transportation Network in Xuzhou City". Or, transport planning as part of the wider discipline of urban planning (and anti-planning).

Contra that dilettante approach, in this piece the FT's Izabella Kaminska interviews an actual professional.

From FT Alphaville:...MORE

Here's one of those quasi-esoteric complexity thingies, from the journal, Nature, December 20, 2017:

Morphology of travel routes and the organization of cities

Abstract

The city is a complex system that evolves through its inherent social and economic interactions. Mediating the movements of people and resources, urban street networks offer a spatial footprint of these activities. Of particular interest is the interplay between street structure and its functional usage. Here, we study the shape of 472,040 spatiotemporally optimized travel routes in the 92 most populated cities in the world, finding that their collective morphology exhibits a directional bias influenced by the attractive (or repulsive) forces resulting from congestion, accessibility, and travel demand. To capture this, we develop a simple geometric measure, inness, that maps this force field. In particular, cities with common inness patterns cluster together in groups that are correlated with their putative stage of urban development as measured by a series of socio-economic and infrastructural indicators, suggesting a strong connection between urban development, increasing physical connectivity, and diversity of road hierarchies.

Introduction

The city is an archetype of a complex system, existing and evolving due to the myriad socio-economic activities of its inhabitants^1,2,3. These activities are mediated by the accessibility of urban spaces depending on the city topography and its infrastructural networks⁴, a key component of which are the roads. Indeed, different street structures result in varying levels of efficiency, accessibility, and usage of the transportation infrastructure^{5,6,7,8,9,10,11}. Structural characteristics, therefore, have been of great interest in the literature^12,13,14,15 and many variants of structural quantities have been proposed and measured in urban contexts, including the degrees of street junctions¹⁶, lengths of road segments¹⁵, cell areas or shapes delineated by streets¹³, anisotropies¹⁴, and network centrality^17,18. Collectively, these structural properties have uncovered unique characteristics of individual cities as well as demonstrated surprising statistical commonalities manifested as scale invariant patterns across different urban contexts^19,20,21.

While these studies have shed light on the statistical structure of street networks, there is limited understanding of the interplay between the road structure and its influence on the movement of people and the corresponding flow of socio-economic activity; that is, the connection between urban dynamics and its associated infrastructure²². One way to tease out this connection is to examine the sampling of routes, that is an examination of how inhabitants of a city potentially utilize the street infrastructure. While a number of studies have been conducted on the empirical factors behind the choice of routes^{23,24,25,26,27}, much remains to be done, in particular, understanding the morphological properties of route choices.

Indeed, the morphology of a route is shaped by the embedded spatial pattern of a city (land use and street topology) in association with dynamical factors such as congestion, accessibility, and travel demand, which relate to various attendant socio-economic factors. Analyzing the morphology of routes, therefore, allows us to potentially uncover the complex interactions that are hidden within the coarse-grained spatial pattern of a city. Furthermore, the morphology also encodes the collective property of routes, including their long-range functional effects. For example, a single street, depending on its connectivity and location, can have influence that spans the dynamics across the whole city (Broadway in New York City for instance)⁵.

In particular, traffic patterns and the shape of routes have been shown to be determined, among other factors, by two competing forces²⁴. On the one hand, one finds an increased tendency of agglomeration of businesses, entertainments, and residential concerns near the urban center, correspondingly leading to a higher density of streets^28,29 and thus attracting traffic and flows toward the interior of the city (positive urban externality). Conversely, this increasing density leads to congestion and increase in travel times (negative urban externality) thus necessitating the need for arterial roads or bypasses along the urban periphery to disperse the congestion at the core. This has the effect of acting as an opposing force, diverting the flow of traffic away from the interior of the city.

Here, we investigate these competing effects through a detailed empirical study of the shape of 472,040 travel routes between origin–destination points in the 92 most populated cities in the globe, representing all six inhabited continents. Each route consists of a series of connected roads; accompanying information on their geographical location, length, and speed limit retrieved from the OpenStreetMap database³⁰. We split our analysis between the shortest routes (necessarily constrained by design limitations and city topography) and the fastest routes (representing the effects of traffic and dynamic route sampling), with the former representing aspects of the city morphology, while the latter in some sense representing the dynamics mediated by the morphology (see Methods for details). Specifically, the shortest routes are a function of the bare road geographic structure, while the fastest routes represent the effective geographic structure—a function of the heterogeneous distribution of traffic velocity resulting from varying transportation efficiency and congestion patterns^31,32,33,34. To uncover the functional morphology of these two categories of routes, we define a geometric metric, which we term inness—a function of both the direction and spatial length of routes—that captures the tendency of travel routes to gravitate toward or away from the city center. This metric serves as a proxy for the geographical distribution of attractive forces that may be implicit in the sampling of streets (as reflected in directional bias) and that otherwise cannot be captured by existing measures. Our analysis represents a step toward the very important challenge of determining the spatial distribution of urban land-use and street topology to balance the inherent negative and positive urban externalities that result from rapid urbanization²⁴.

Results 
Definition of inness I

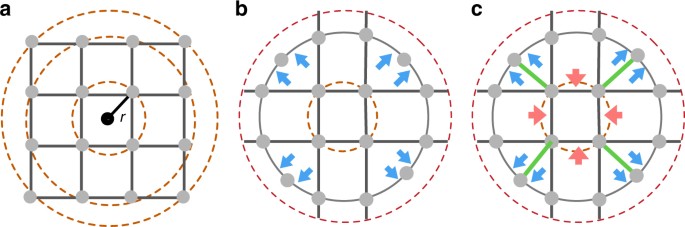
Figure 1 illustrates the forces related to a city’s morphological patterns shaped by infrastructural and socio-economic layouts. For the case of a square grid, as shown in Fig. 1a, the shortest routes between any two points at a distance r either correspond trivially to the line connecting them directly, or are degenerate paths that traverse the grid in either direction. Taking the average of the multiple paths cancels any directional bias relative to the center of the grid. Yet, a small perturbation of this regularity can change this neutral feature dramatically, as shown in Fig. 1b, where we shift the four outermost points inward as to place them on the second ring from the center. Points lying on this ring have shortest routes that lie along the periphery, thus introducing a dispersive force away from the center (marked as blue arrows). In Fig. 1c, we further perturb the topology by adding four lines from the outer ring to the inner ring (marked in green) thus increasing connectivity toward the center. Shortest paths between pairs on the outer ring traverse through the inner ring and are curved toward the city center, resulting in an attractive force (represented as red arrows). Beyond this simple example, which is primarily a function of topology and is applicable to shortest paths, other factors are in play such as travel time and route velocity as considered in ref. ²⁴, that will necessarily affect the patterns seen in fastest paths. Furthermore, the illustration assumes a single center of gravity, as it were, whereas such an effect may manifest itself at multiple scales, resulting in cancellation of any measurable force toward a putative city center.

Fig. 1

Biasing forces found in urban morphology. Three schematic urban street arrangements share similar topological structure, but different geometric layouts resulting in varying dynamics. a A grid structure where the shortest paths between points at the same radius show no directional bias. b Repulsive forces relative to the origin (marked in blue) emerge as we break the grid symmetry by relocating the four outer points on the inner equidistant ring line. Paths lying on this ring now have the shortest paths that traverse the periphery and avoid the center. c Further perturbing the topology by increasing connectivity to the center (marked as four green lines) now leads to shortest paths that go through the center as if an attractive force is present (marked in red)

...MUCH MORE

Previously, here are a couple posts from 2017, there are quite a few in prior years as well:
"City Travel Scaling"
Today On Book Nook, the FT's Izabella Kaminska Reviews "Scale" (Why Cities Keep Growing, Corporations And People Always Die, And Life Gets Faster*)