How could anyone resist reading a Wikipedia article titled “Homicidal Chauffeur problem?” I couldn’t! I learned that it was a math problem posed in 1951 by game theorist Rufus Isaacs in his paper for the RAND Corporation called “Games of Pursuit.”
The problem takes place in a parking lot, empty except for a person on foot (the evader, designated by the letter E) and a homicidal chauffeur (the pursuer, P) who wants to run over the evader. P is faster than the E, but E can make tighter turns while running. With E’s “only hope being delay until rescue,” what is the best strategy to avoid being run over?
“Some qualitative aspects are evident,” wrote Isaacs. “If E is more or less in front of P the situation is simple; E will flee and P will follow.” Because P is faster, E is doomed.
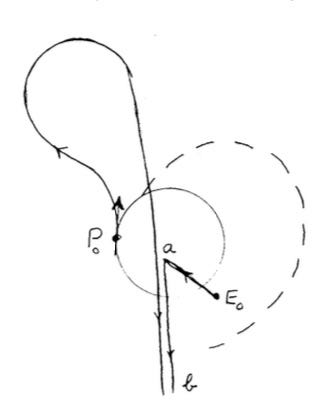
But what if the chase begins with the evader behind the pursuer? Isaacs included a hand-drawn illustration in his paper to explore this scenario (shown above). P0 and E0 are the starting positions of the pursuer and the evader. If E can get inside the circle of P’s turning radius (shown in the figure as the solid circle), they can avoid being hit. But if P is smart enough to first turn away from E and “then swerve about and pursue directly,” then E will have to run toward P in an attempt to stay inside the car’s turning radius. “But as P starts to swerve, E (now at [.a]) turns tail and flees until capture is consummated near b.”
To determine E’s best strategy for staying alive as long as possible, Isaacs developed a solution that started with the desired outcome and worked backward to find the optimal strategy — the best moves for both pursuer and evader where neither can do better by changing their approach. This is called a “Nash equilibrium” in game theory.
Origins of Game Theory
The RAND corporation wasn’t interested in helping people learn how to evade homicidal chauffeurs. They were interested in military problems, like how a nimble fighter jet could outmaneuver a faster but less nimble heat-seeking missile. The Homicidal Chauffeur was just one of many problems that RAND was exploring while developing the foundations of Game Theory, the study of how people and organizations make decisions where success depends not just on your own decisions, but on anticipating and responding to what others will do....
....MUCH MORE